Trigonometric levelling is an ingenious indirect method in surveying for determining the relative elevations of points by precisely measuring vertical angles and horizontal distances. Unlike direct levelling, which uses horizontal lines of sight, trigonometric levelling leverages principles of trigonometry, making it invaluable for measuring heights of inaccessible objects, tall structures, or across challenging terrains. This infographic unravels its core principles, key concepts, detailed procedures for various field situations, and provides critical insights for civil engineers.
Fundamentals of Trigonometric Levelling
Trigonometric levelling is an **indirect method** where elevations are determined using a theodolite to measure vertical angles and a tape, chain, or tacheometer to measure horizontal distances. The difference in elevation is then calculated using trigonometric ratios.
While not as accurate as direct levelling for short, flat distances, it is indispensable for **topographic work**, determining heights of tall structures (e.g., chimneys, towers), or surveying where direct levelling is impractical or impossible due to obstacles or terrain.
Key Terms & Concepts
Understanding these fundamental terms is crucial for performing and interpreting trigonometric levelling measurements.
| Term | Description | Visual Representation |
|---|---|---|
| Angle of Elevation (α) | The vertical angle measured upwards from the horizontal line of sight to a point above the instrument’s horizontal plane. | ↗️ |
| Angle of Depression (β) | The vertical angle measured downwards from the horizontal line of sight to a point below the instrument’s horizontal plane. | ↘️ |
| Line of Sight | The imaginary line extending from the optical center of the objective lens to the point sighted. For trigonometric levelling, this line is inclined. | ― – – – → |
| Horizontal Distance (D) | The true horizontal distance between the instrument station and the object whose elevation is being determined. Crucial for trigonometric calculations. | ⟷ |
| Height of Instrument (hi) | The vertical distance from the datum to the horizontal axis of the telescope of the theodolite. | ↕️ |
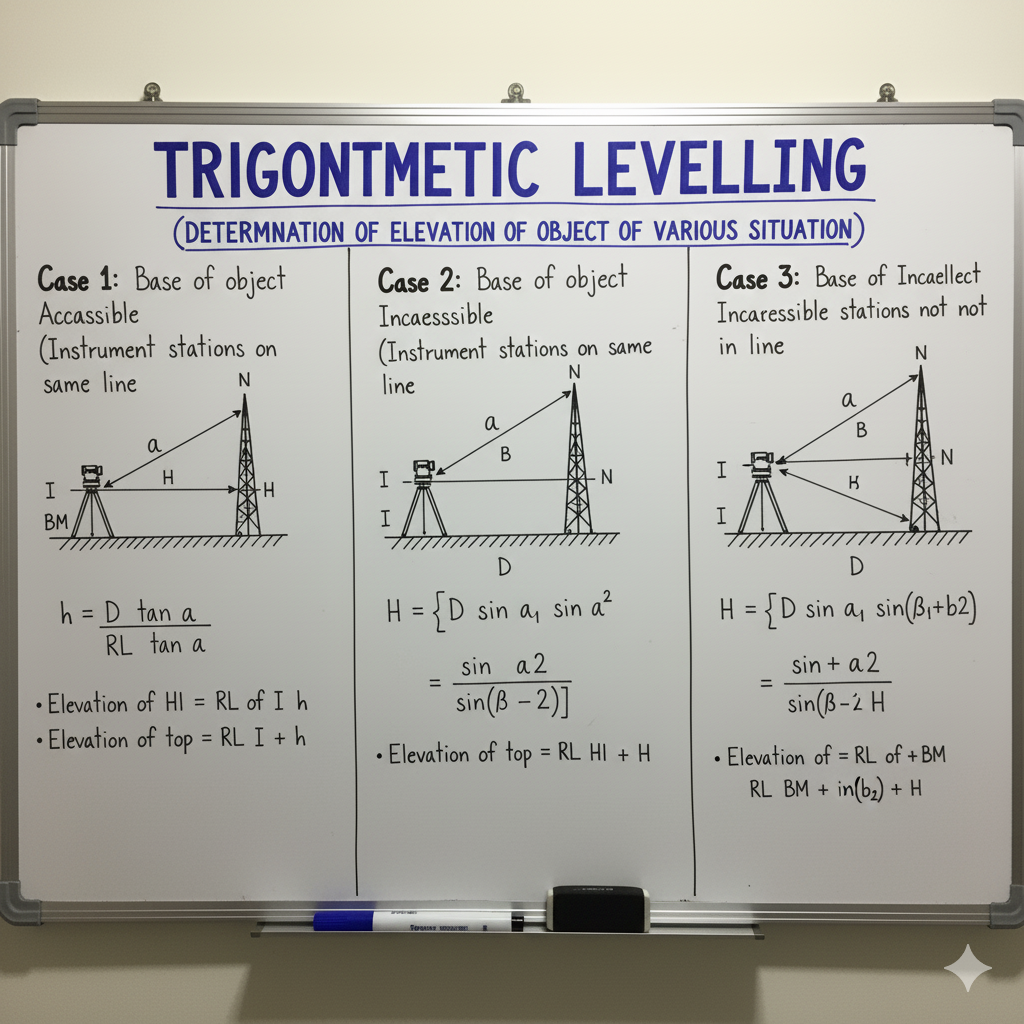
Elevation Determination: Base of Object Accessible
This is the simplest case where the horizontal distance to the object can be measured directly.
Method: Instrument at A, Staff at B (Basic Levelling)
The difference in elevation between two points (A and B) can be determined by setting up the instrument at A, taking a staff reading at B, and measuring the vertical angle to a point on the staff at B.
Vertical height (V) = D × tan(θ)
RL of B = RL of A + hi + V – Staff Reading at B
Elevation Determination: Base Inaccessible (Single Instrument Setup)
Used for determining the height of tall structures (e.g., towers, chimneys) where the base is inaccessible, but the top is visible from a single instrument station.
Procedure & Formula
Set up the theodolite at a station P (RL known) and accurately level it.
Measure the height of the instrument (hi).
Take a staff reading on a benchmark (BM) or known point to find RL of the instrument’s horizontal axis.
Measure the horizontal distance (D) from P to the object’s base (or perpendicular to a point on the base if direct measurement is not possible).
Measure the vertical angle (α) to the top of the object from the horizontal axis.
Vertical height (V) = D × tan(α)
RL of Top of Object = RL of P + hi + V
Elevation: Base Inaccessible (Two Setups – Same Vertical Plane)
This method is used when the base of the object is inaccessible, and two instrument setups are required, both lying in the same vertical plane as the object’s base.
Procedure & Formula
Set up theodolite at station A, measure hi1, and sight to the top of the object (T), measuring vertical angle α1.
Set up at station B (at a known horizontal distance ‘b’ from A, along the line of sight to the object or its projection), measure hi2, and sight to T, measuring vertical angle α2.
Take staff readings on a known point (or reciprocal staff readings between A and B) to establish relative RLs of instrument axes.
Let H be the height of the object above the horizontal plane of lower instrument.
If both instruments are at same height, H = b × (tan(α1) × tan(α2)) / (tan(α1) – tan(α2))
RL of Top = RL of instrument axis + H
Note: The exact formula depends on whether the stations are on the same side or opposite sides of the object, and whether the instrument axes are at the same or different RLs. The general principle involves solving two simultaneous equations.
Elevation: Base Inaccessible (Two Setups – NOT in Same Vertical Plane)
This advanced case is used when the base is inaccessible, and the two instrument setups cannot be placed in the same vertical plane as the object. This often occurs when there are obstacles in the line of sight.
Procedure & Formula
Establish two instrument stations A and B, whose horizontal distance ‘b’ is known.
From A, measure vertical angle α1 to the object’s top (T) and horizontal angle θA from AB to AT.
From B, measure vertical angle α2 to the object’s top (T) and horizontal angle θB from BA to BT.
Determine the RL of the instrument axes (hiA, hiB) using a known benchmark.
First, calculate horizontal distances DA and DB using sine rule in triangle ABT:
DA / sin(θB) = DB / sin(θA) = b / sin(180° – θA – θB)
Then, Vertical height (VA) = DA × tan(α1)
RL of Top = RL of A + hiA + VA
(This can be cross-checked with VB = DB × tan(α2) and RL from B)
Advantages & Disadvantages of Trigonometric Levelling
Understanding the pros and cons helps in judiciously choosing this method over direct levelling.
| Aspect | Advantages | Disadvantages |
|---|---|---|
| Applicability | Ideal for inaccessible points, tall structures, and undulating terrain. | Less accurate than direct levelling for short distances or flat ground. |
| Speed | Faster for rough levelling over large areas or across obstacles. | Requires accurate horizontal distance measurement, which can be time-consuming for inaccessible bases. |
| Obstacles | Can be performed across rivers, valleys, or dense foliage where direct levelling is not feasible. | Accuracy is affected by atmospheric refraction and Earth’s curvature (though corrections can be applied). |
| Equipment | Only a theodolite and a measuring tape/EDM are needed. | Requires skilled operators to measure angles and distances precisely. |
GATE Exam Practice Questions & Explanations
Test your understanding of Trigonometric Levelling concepts and calculations with these GATE-style questions.
1. Trigonometric levelling is a type of:
Answer: Indirect levelling
Unlike direct levelling, it calculates elevation differences using measured angles and distances, rather than direct staff readings along a horizontal line of sight.
2. The instrument primarily used for measuring vertical angles in trigonometric levelling is a:
Answer: Theodolite
A theodolite is essential for precise measurement of both horizontal and vertical angles.
3. If the horizontal distance to an object is ‘D’ and the angle of elevation to its top is ‘α’, the vertical height (V) from the instrument axis to the top is given by:
Answer: V = D * tan(α)
This is the fundamental trigonometric relationship for height calculation when the angle of elevation and horizontal distance are known.
4. Trigonometric levelling is particularly suitable for determining the height of:
Answer: Tall structures like chimneys or towers
Its indirect nature allows for measurement of inaccessible heights, which is a major advantage over direct levelling for such objects.
5. The angle measured downwards from the horizontal line of sight to a point below is called:
Answer: Angle of Depression
This is the definition of an angle of depression, used when sighting points below the instrument’s horizontal plane.
6. For a point B, its RL is 100m. The instrument is set up at A, its height of instrument (hi) is 1.5m. The horizontal distance AB is 50m, and the angle of elevation to B is 10°. The RL of B is (ignoring Earth’s curvature and refraction):
Answer: This question is incomplete as RL of A is needed to calculate RL of B. If the question implicitly asks for RL of B from A, then RL of B = RL_A + hi + D*tan(angle). Without RL of A, it’s not possible to provide RL of B.
The question assumes an instrument set up at A, but then asks for the RL of B based on an initial RL of B. Assuming it meant RL of A is 100m: RL of B = 100 + 1.5 + 50 * tan(10°) = 101.5 + 50 * 0.1763 = 101.5 + 8.815 = 110.315 m.
7. When the base of an object is inaccessible, and two instrument setups are in the same vertical plane as the object, what is eliminated in the calculation of height difference if the instrument heights are equal?
Answer: Errors due to Earth’s curvature and refraction
By taking readings from two points in the same vertical plane, the effect of curvature and refraction on both lines of sight can be effectively cancelled out in the calculation.
8. What is the main disadvantage of trigonometric levelling compared to direct levelling?
Answer: Generally less accurate for short distances or flat ground.
Direct levelling is more precise for precise elevation determination over short distances due to its direct measurement approach.
9. For determining the height of a hill peak where its base is inaccessible, which method of trigonometric levelling is most suitable?
Answer: Two instrument setups, base inaccessible (either same or different vertical planes).
A single setup often requires a measurable horizontal distance to the base. For inaccessible bases, two setups provide the necessary geometric solution.
10. The height of instrument (hi) is the vertical distance from the datum to the:
Answer: Horizontal axis of the telescope of the theodolite
It is the elevation of the line of sight (or collimation axis) of the instrument.
11. In trigonometric levelling, if the staff reading at a point is taken as zero, it means the line of sight passes:
Answer: Through the point on the staff that is at the same elevation as the instrument’s horizontal axis.
A zero staff reading implies the line of sight directly hits the base of the staff when the instrument is perfectly level and aligned with the staff’s base.
12. The accuracy of trigonometric levelling is greatly affected by:
Answer: Atmospheric refraction
Refraction causes the line of sight to bend, directly impacting the measured vertical angles and hence the calculated heights. Corrections are essential.
13. Which scenario of trigonometric levelling is generally solved by setting up two simultaneous equations?
Answer: Base inaccessible, two instrument setups in the same vertical plane (different instrument heights).
When instrument heights differ, a system of equations is required to solve for the unknown height of the object and the unknown horizontal distance.
14. For long sights in trigonometric levelling, what correction is important to apply?
Answer: Curvature and refraction corrections
Over long distances, the Earth’s curvature and atmospheric refraction significantly affect the line of sight, requiring precise corrections.
15. If the angle of depression to the base of an inaccessible object is ‘β’, and the horizontal distance to it is ‘D’, the vertical drop from the instrument axis to the base is:
Answer: D * tan(β)
This is the direct trigonometric calculation for vertical distance when sighting downwards from a known horizontal distance.
16. The vertical distance between the instrument’s horizontal axis and the point sighted is called the:
Answer: Vertical Height (V)
This is the component of the sight that represents the height difference between the instrument’s line of sight and the sighted point, before adding/subtracting instrument height or staff reading.
17. When two instrument setups for an inaccessible object are NOT in the same vertical plane, which type of angle measurement becomes crucial for determining horizontal distances to the object?
Answer: Horizontal angles to the object from both instrument stations
These horizontal angles, along with the baseline between the two instrument stations, form a triangle that can be solved using the sine rule to find the horizontal distances to the object.
18. If the RL of the instrument axis is 150.00m, and the angle of elevation to the top of a tower is 20° from a horizontal distance of 100m, the RL of the top of the tower (ignoring C&R) is:
Answer: 186.42 m
RL of top = RLaxis + D * tan(α) = 150 + 100 * tan(20°) = 150 + 100 * 0.36397 = 150 + 36.397 = 186.397 ≈ 186.42 m.
19. In a trigonometric levelling setup, if the object’s top is sighted and the base is accessible, the final RL calculation involves:
Answer: RL of instrument station + height of instrument + D*tan(angle) – staff reading at object base.
This combines the known RL, instrument height, vertical height calculated, and the staff reading at the base to get the final RL of the object’s base.
20. What is a key advantage of trigonometric levelling over direct levelling for extensive topographic mapping?
Answer: Faster data collection over large or undulating areas.
While less precise for spot heights, it offers greater efficiency for mapping broad topographical features by measuring angles and distances from a few strategic points.