Triangulation is a foundational surveying technique for establishing precise control networks over large areas. It involves creating a series of interconnected triangles, where only one side (the baseline) is measured directly, and all angles are measured accurately. This method then uses trigonometric principles to compute the lengths of all other sides and the coordinates of all stations. This infographic explores the principles, classification, layout types, and key concepts like well-conditioned triangles, along with an introduction to its modern counterpart, Trilateration.
What is Triangulation?
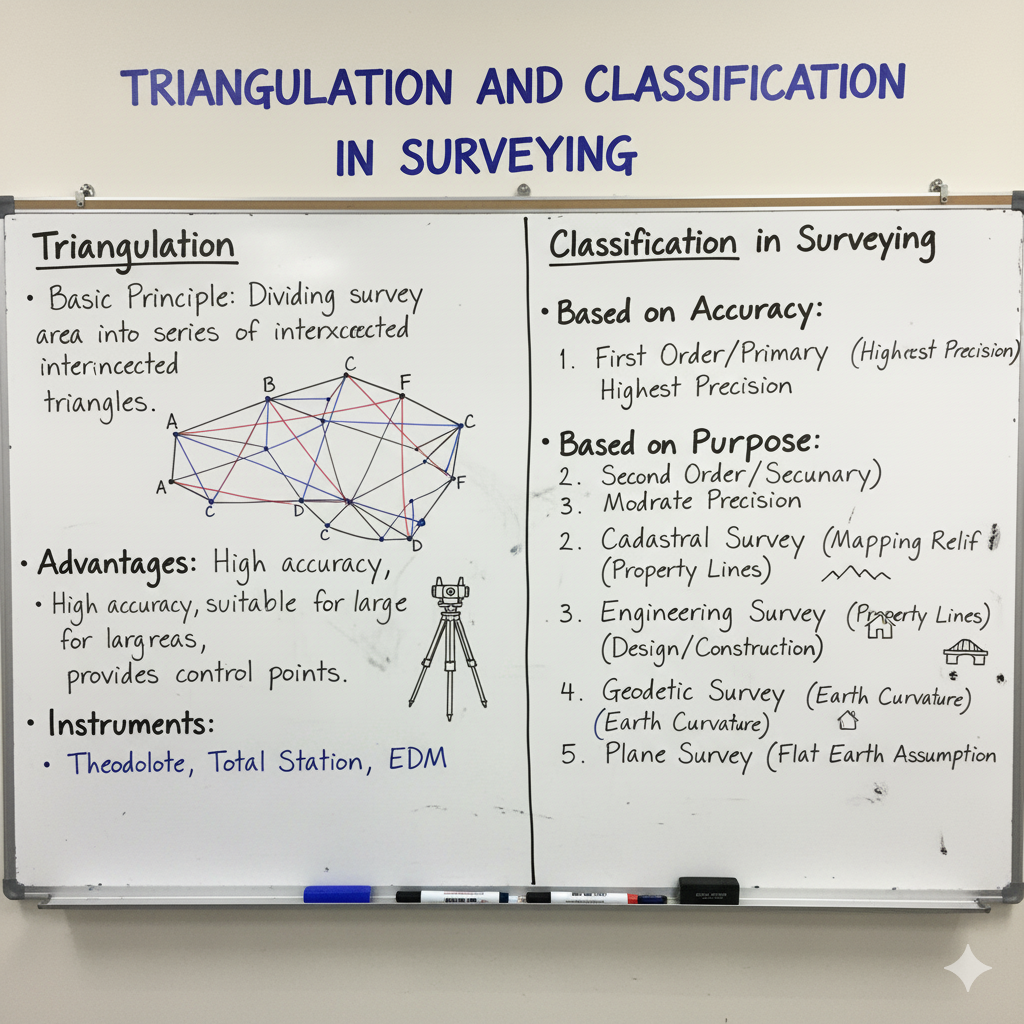
Triangulation is a method of surveying where the area is covered by a network of triangles. In this network, the lengths of all sides are determined from the measurement of only one side (called the base line) and all the angles of the triangles.
The principle relies on trigonometry: if one side and all angles of a triangle are known, the other two sides can be calculated. This forms a robust framework for establishing control points over vast regions, particularly useful for geographical surveys, mapping, and engineering projects requiring high accuracy.
Classification of Triangulation Systems (Orders of Precision)
Triangulation systems are classified into different orders based on the required precision, the extent of the area covered, and the purpose of the survey.
| Classification | Description | Purpose / Applicability | Precision Level (Typical) |
|---|---|---|---|
| Primary / 1st Order | Highest order of triangulation, covering very large areas (e.g., entire countries). Involves long baselines and rigorous observations. | Establishment of national geodetic control networks, fundamental for all other surveys. | Very High (1 in 50,000 to 1 in 250,000) |
| Secondary / 2nd Order | Intermediate precision, used to densify the primary network. Covers smaller areas than primary, with shorter baselines. | Extension of primary control, mapping large regions, engineering projects. | High (1 in 10,000 to 1 in 50,000) |
| Tertiary / 3rd Order | Lowest order of precision for general purposes, used to establish dense control points for local surveys. Involves shortest baselines. | Local surveys, detailed mapping, engineering layout for specific projects (e.g., bridge, dam). | Moderate (1 in 3,000 to 1 in 10,000) |
Common Triangulation Layout Patterns
The arrangement of triangles in a triangulation network is crucial for efficiency, accuracy, and providing internal checks.
| Layout Type | Description | Advantages / Use Case | Conceptual Diagram |
|---|---|---|---|
| Single Chain of Triangles | A series of interconnected triangles forming a linear chain. | Economical for narrow strips of land (e.g., roads, rivers). | △-△-△-△ |
| Braced Quadrilaterals | Consists of four stations forming a quadrilateral with both diagonals observed. | Offers excellent checks (8 angles, 4 sides, 2 diagonals), robust, highly accurate. Best layout for primary and secondary work. | ▰ |
| Centered Triangles / Polygons | A central station from which lines are run to other stations forming a polygon (e.g., hexagon, octagon). All angles and sides of polygon and central triangles are observed. | Suitable for large, open areas. Provides strong figures and good checks. | ⏺️-△-⏺️ |
| Chain of Polygons | Combination of polygons forming a chain, often used for very wide areas. | Provides stronger figures and more checks than simple chains. | ⬡-⬡-⬡ |
Well-Conditioned Triangle: The Ideal Figure
In triangulation, the shape of the triangles significantly impacts the accuracy of computed sides. A “well-conditioned” triangle minimizes the effect of errors in angular measurements on the calculated lengths.
Definition & Importance:
- A well-conditioned triangle is one where any small error in the angular measurement will produce the least possible error in the computed lengths of its sides.
- This minimizes error propagation through the network.
Criteria for Well-Conditioned Triangle:
- Ideal Shape: An equilateral triangle (all angles 60°). This is mathematically the strongest figure.
- Practical Rule: Angles should generally not be less than 30° or more than 120°.
- Triangles with angles outside this range (e.g., very acute or obtuse) are “ill-conditioned” and should be avoided or re-observed carefully.
Trilateration: An Evolution in Control Surveying
Trilateration is a modern control survey method that leverages technological advancements in distance measurement, offering an alternative to traditional triangulation.
| Concept | Description | Key Difference from Triangulation |
|---|---|---|
| Definition | A control survey method where a network of triangles is established, but unlike triangulation, **all three sides of every triangle are precisely measured** using Electronic Distance Measurement (EDM) instruments. No angular measurements are taken in the field. | Triangulation: Measures all angles, measures only one baseline directly. Trilateration: Measures all sides directly, measures no angles. |
| Primary Instrument | Electronic Distance Measurement (EDM) devices or Total Stations. | |
| Accuracy | Can achieve very high accuracy due to precise EDM measurements. Less susceptible to atmospheric refraction errors that affect angular measurements over long distances. | |
| Application | Establishment of high-precision control networks, especially where angular measurements are difficult or time-consuming. |
Advantages & Disadvantages of Triangulation
Despite the rise of modern techniques, understanding triangulation’s benefits and limitations remains crucial for civil engineers.
| Aspect | Advantages | Disadvantages |
|---|---|---|
| Accuracy | Provides very high accuracy over large areas by distributing errors effectively through the network. | Highly dependent on atmospheric conditions (refraction) for accurate angular measurements, especially for long sights. |
| Error Checks | Offers numerous checks (sum of angles in a triangle, angular closure in polygons) for internal consistency. | Requires clear lines of sight between stations, which can be obstructed by terrain or vegetation, necessitating signal towers. |
| Cost | Can be economical for extensive surveys as fewer linear measurements (only baselines) are needed. | Fieldwork can be time-consuming due to precise angular measurements and station setup. |
| Rigorous Adjustment | Data can be subjected to rigorous least squares adjustment for optimal results. | Not ideal for undulating or very rough terrain where line of sight is frequently obstructed. |
| Basis for Mapping | Forms the primary framework for large-scale mapping projects. | Requires a well-conditioned network of triangles for optimal accuracy. |
GATE Exam Practice Questions & Explanations
Test your understanding of Triangulation, its principles, types, and related concepts with these GATE-style questions.
1. In a triangulation survey, the lengths of all sides are determined from the measurement of:
Answer: Only one side (the base line) and all angles of the triangles.
This is the defining principle of triangulation, where only one side is directly measured, and others are computed using trigonometry.
2. For a well-conditioned triangle, the angles should preferably be:
Answer: Between 30° and 120°
This range ensures that errors in angle measurement have the least possible effect on the computed lengths of the sides, minimizing error propagation.
{/* 30° is the minimum angle for a well-conditioned triangle. */}
3. The highest order of triangulation, used for establishing national geodetic control networks, is:
Answer: Primary (1st Order) Triangulation
Primary triangulation aims for the highest precision to establish a fundamental framework for all other surveys.
4. Which triangulation layout offers the most rigorous checks and is highly robust?
Answer: Braced Quadrilaterals
With both diagonals observed, braced quadrilaterals provide numerous geometric conditions for checking and adjusting observations, leading to high accuracy.
5. In trilateration, what measurements are taken in the field?
Answer: All three sides of the triangles are precisely measured.
Trilateration is distinct from triangulation because it relies solely on direct distance measurements, with no angles measured in the field.
6. An equilateral triangle is considered ideal for a triangulation network because:
Answer: It is mathematically the strongest figure for minimizing error propagation.
In an equilateral triangle (all angles 60°), errors in angle measurements have the least impact on the computed side lengths.
7. Secondary (2nd Order) triangulation is typically used for:
Answer: Densifying the primary network and mapping large regions.
It extends the higher-order control to provide a denser network for subsequent, more detailed surveys.
8. A single chain of triangles layout is most economical for:
Answer: Narrow strips of land like roads or rivers.
Its linear nature makes it efficient for surveying long, narrow features.
9. Which of the following is a disadvantage of triangulation?
Answer: Requires clear lines of sight between stations, which can be obstructed.
Visibility between stations is critical for angular measurements, often necessitating clearing or building signal towers.
10. If an error in angular measurement leads to a large error in computed length, the triangle is considered:
Answer: Ill-conditioned
Ill-conditioned triangles (e.g., with very acute or very obtuse angles) are prone to significant error propagation.
11. What is the key advantage of Trilateration over Triangulation?
Answer: Less susceptible to atmospheric refraction errors affecting angular measurements.
Since trilateration measures distances directly using EDM, it avoids the angular refraction issues that can affect triangulation over long sights.
12. Tertiary (3rd Order) triangulation is typically used for achieving precision of:
Answer: Moderate (1 in 3,000 to 1 in 10,000)
It provides a denser network for local surveys but with lower precision requirements than primary or secondary orders.
13. In a centered polygon layout, what measurements are taken from the central station?
Answer: Lines are run to other stations, and all angles and sides of the polygon and central triangles are observed.
The central station serves as a common point for observation to all vertices of the polygon.
14. What is the fundamental difference in fieldwork between triangulation and trilateration?
Answer: Triangulation measures angles, trilateration measures distances.
This is the core distinction between the two methods of establishing a control network.
15. A triangulation network’s accuracy is primarily dependent on the precision of its:
Answer: Angular measurements
Since lengths are computed from angles and one baseline, accurate angle measurement is paramount for overall network accuracy in triangulation.
16. The precision level of Primary Triangulation ranges from:
Answer: 1 in 50,000 to 1 in 250,000
This indicates the extremely high level of accuracy required for national geodetic control.
17. Which triangulation layout is considered the strongest and most suitable for primary and secondary work?
Answer: Braced Quadrilaterals
Their geometric redundancy provides excellent internal checks and error distribution.
18. Trilateration utilizes which primary instrument for measurement?
Answer: Electronic Distance Measurement (EDM) devices or Total Stations.
These instruments enable the direct and precise measurement of all side lengths in the triangular network.
19. The process of establishing a framework of control points over large areas by a network of triangles is generally referred to as:
Answer: Triangulation
This defines the core purpose and methodology of triangulation in surveying.
20. Which type of triangle should be avoided in a triangulation network for accurate results?
Answer: Ill-conditioned triangles (e.g., very acute or very obtuse angles).
These shapes are prone to significant error propagation from small angular measurement errors.