Traverse surveying is a cornerstone of modern civil engineering, forming the backbone for mapping and construction layouts. It involves measuring the lengths and directions of a series of connected lines. Crucially, raw field data from traverses inevitably contain errors. This infographic comprehensively explains the concepts of Latitude and Departure, quantifies survey accuracy through Closing Error and Relative Precision, and details the essential adjustment rules—Bowditch’s Rule and Transit Rule—used to balance these errors and ensure precise spatial data for design and execution.
Traverse Survey Fundamentals
A traverse is a sequence of interconnected survey lines whose lengths and directions (bearings or angles) are measured. It establishes a framework of control points used for mapping and setting out construction elements.
Fieldwork Steps in Theodolite Traverse
- Reconnaissance: Preliminary inspection to select and mark suitable traverse stations.
- Selection & Marking of Survey Stations: Permanent establishment of stations with pegs or marks.
- Running & Measuring Traverse Lines: Measuring the length of each line using tapes/EDMs.
- Angular Measurements: Measuring interior or exterior angles at each station using a theodolite, or bearings using a compass.
- Marking Offsets: Taking lateral measurements to locate ground features or details relative to the traverse lines.
- Field Book Recording: Meticulous documentation of all measurements, sketches, and remarks.
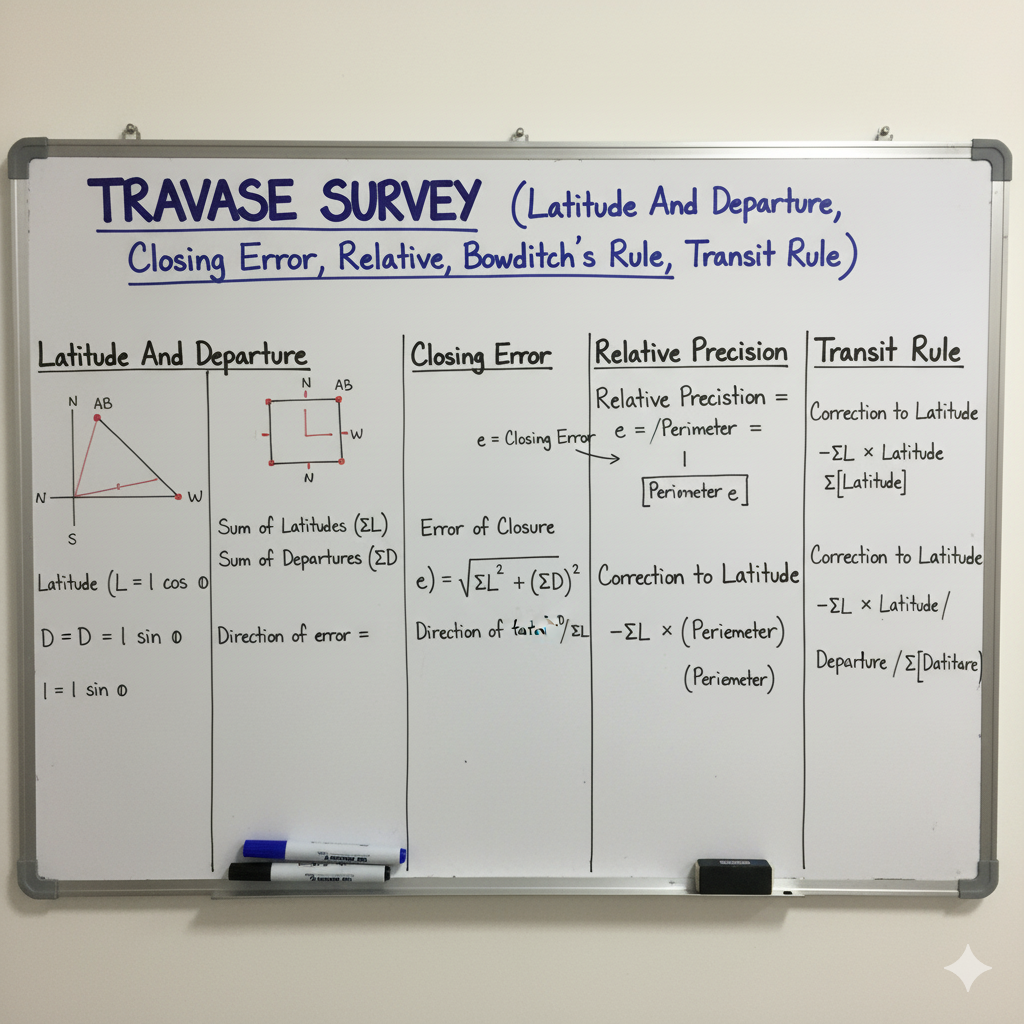
Latitude and Departure: Positional Projections
Latitude and Departure are the rectangular components of a traverse line, representing its projection onto the North-South and East-West axes, respectively. They are fundamental for coordinate computation and traverse adjustments.
| Concept | Definition | Formula (for line L with WCB θ) | Sign Convention |
|---|---|---|---|
| Latitude (L) | The projection of a survey line on the North-South meridian. It is the North-South component. | L = length × cos(θ) | +ve for Northings (N), -ve for Southings (S) |
| Departure (D) | The projection of a survey line on the East-West line. It is the East-West component. | D = length × sin(θ) | +ve for Eastings (E), -ve for Westings (W) |
| Sum of Latitudes (ΣL) | For a closed traverse, the algebraic sum of all latitudes should ideally be zero. | ΣL = 0 (for perfect closure) | Used to check for linear closure in the N-S direction. |
| Sum of Departures (ΣD) | For a closed traverse, the algebraic sum of all departures should ideally be zero. | ΣD = 0 (for perfect closure) | Used to check for linear closure in the E-W direction. |
Closing Error & Relative Precision
In a closed traverse, due to errors in measurement, the end point rarely coincides with the starting point. This discrepancy is known as the closing error, and its magnitude helps determine the survey’s precision.
| Concept | Definition / Formula | Significance |
|---|---|---|
| Linear Error of Closure (E) | The straight-line distance between the actual closing point and the starting point (or known ending point) of a closed traverse. | E = sqrt[ (ΣL)2 + (ΣD)2 ] |
| Direction of Closing Error (α) | The direction of the line representing the closing error, relative to the meridian. | tan(α) = |ΣD / ΣL| |
| Relative Precision (P) | The ratio of the linear error of closure (E) to the perimeter (P) of the traverse. Expressed as 1 in X (e.g., 1 in 5000). | P = E / Perimeter = 1 / (Perimeter / E) |
| Importance | The relative precision indicates the overall accuracy of the traverse survey. A smaller ratio (e.g., 1 in 10,000) indicates higher precision. | Determines if the survey meets specified standards for accuracy; guides selection of adjustment rule. |
Balancing a Traverse: Distributing Errors
Balancing a traverse involves distributing the closing error among the traverse lines proportionally, adjusting their latitudes and departures so that the sum of latitudes and sum of departures both become zero. This ensures the traverse mathematically closes, providing adjusted coordinates for all stations. Two common methods are Bowditch’s Rule and Transit Rule.
Bowditch’s Rule (Compass Rule)
Bowditch’s Rule is one of the most common methods for adjusting a closed traverse. It assumes that errors in both linear (chaining) and angular (compass) measurements are proportional to the square root of the length of the line.
| Aspect | Description | Formula |
|---|---|---|
| Application Condition | Used when linear and angular measurements are presumed to have equal precision, or when the survey is conducted with a compass and chain. | EL ∝ sqrt(L) EA ∝ sqrt(N) |
| Correction to Latitude (CL) | The correction to the latitude of a traverse line. | CL = – (ΣL / Perimeter) × length of line |
| Correction to Departure (CD) | The correction to the departure of a traverse line. | CD = – (ΣD / Perimeter) × length of line |
| Principle | The total error in latitude (ΣL) and total error in departure (ΣD) are distributed proportionally to the length of each traverse line. | Balances both latitudes and departures, ensuring angular and linear closures. |
Transit Rule
The Transit Rule is another method for balancing a closed traverse. It is applied when angular measurements are considered more precise than linear measurements, or when a transit/theodolite is used for angles and a chain/tape for lengths.
| Aspect | Description | Formula |
|---|---|---|
| Application Condition | Used when angular measurements are more precise than linear measurements (e.g., using a theodolite for angles and a chain for lengths). | EL ∝ L EA ∝ N |
| Correction to Latitude (CL) | The correction to the latitude of a traverse line. | CL = – (ΣL / Σ|Latitude|) × |latitude of line| |
| Correction to Departure (CD) | The correction to the departure of a traverse line. | CD = – (ΣD / Σ|Departure|) × |departure of line| |
| Principle | Errors in latitude are distributed proportionally to the absolute value of the latitude of each line, and errors in departure are distributed proportionally to the absolute value of the departure of each line. | Maintains the original angles of the traverse more closely. |
Comparative Analysis: Bowditch’s Rule vs. Transit Rule
Choosing between Bowditch’s Rule and Transit Rule depends on the relative precision of angular and linear measurements in the traverse.
| Feature | Bowditch’s Rule | Transit Rule |
|---|---|---|
| Assumed Precision | Linear and angular measurements have equal precision. | Angular measurements are more precise than linear measurements. |
| Error Distribution | Error is distributed proportionally to the length of the line. | Error is distributed proportionally to the latitude/departure of the line. |
| Suitable Instruments | Compass and chain survey. | Theodolite/transit and tape/chain survey. |
| Impact on Angles | Balances angles and lengths simultaneously. | Tends to keep the original angles relatively unchanged. |
| Common Use Case | General purpose traverses, particularly when using less precise angular instruments. | Traverses where angular measurements are taken with high precision. |
GATE Exam Practice Questions & Explanations
Test your understanding of traverse surveying, latitude, departure, closing error, and adjustment rules with these GATE-style questions.
1. For a closed traverse, the algebraic sum of latitudes should ideally be:
Answer: Zero
In a perfectly closed traverse, the sum of all northings should equal the sum of all southings, resulting in a net latitude of zero.
2. Bowditch’s Rule is generally applied when:
Answer: Linear and angular measurements have equal precision.
This rule assumes that both types of measurements contribute equally to the total error, making it suitable for chain and compass surveys.
3. The projection of a survey line on the East-West axis is known as its:
Answer: Departure
Departure represents the Easting or Westing component of a traverse line.
4. If the sum of latitudes (ΣL) is 0.5m and sum of departures (ΣD) is 1.2m for a closed traverse, the linear error of closure (E) is approximately:
Answer: 1.3m
E = sqrt(ΣL² + ΣD²) = sqrt(0.5² + 1.2²) = sqrt(0.25 + 1.44) = sqrt(1.69) = 1.3m.
5. The Transit Rule is used when:
Answer: Angular measurements are more precise than linear measurements.
This rule is preferred for surveys where angles are measured with a high-precision instrument like a theodolite, and distances with a tape/chain.
6. Relative precision of a traverse is expressed as:
Answer: Ratio of linear error of closure to the perimeter of the traverse (1 in X).
It quantifies the accuracy of the traverse relative to its total length, providing a standard for comparison.
7. In Bowditch’s Rule, the correction to latitude or departure of a line is proportional to its:
Answer: Length
Bowditch’s rule distributes errors based on the length of each line in the traverse.
8. A series of connected survey lines whose lengths and directions are measured is called a:
Answer: Traverse
This is the definition of a traverse, which forms the framework of many surveys.
9. If a traverse starts and ends at a known point (with known coordinates), it is a:
Answer: Closed Traverse
Closed traverses allow for checking of angular and linear errors, making them more verifiable.
10. In the Transit Rule, the correction to the latitude of a line is proportional to its:
Answer: Absolute latitude
The Transit Rule distributes errors in latitude based on the magnitude of the latitude component of each line.
11. A traverse that starts from a known point but ends at an unknown location is an:
Answer: Open Traverse
Open traverses are commonly used for linear features like roads or canals, but they do not provide a direct check for closure errors.
12. The main objective of balancing a traverse is to:
Answer: Distribute the closing error among the traverse lines and make sums of latitudes and departures zero.
Balancing ensures that the traverse mathematically closes, providing adjusted and consistent coordinates for all stations.
13. Which of the following is an assumption of Bowditch’s rule regarding error sources?
Answer: Errors in both linear and angular measurements are proportional to the square root of the length of the line.
This assumption underlies the distribution logic of Bowditch’s rule.
14. If the perimeter of a traverse is 1000m and the linear error of closure is 0.1m, its relative precision is:
Answer: 1 in 10000
Relative Precision = Perimeter / E = 1000 / 0.1 = 10000. So, 1 in 10000.
15. The Transit Rule tends to keep which aspect of the original traverse unchanged to a greater extent?
Answer: The original angles of the traverse.
Because Transit Rule distributes errors based on latitudes and departures, it affects the lengths more significantly than the angles, thus preserving angular precision.
16. Latitude is the projection of a line on which axis?
Answer: North-South axis
Latitude gives the Northing or Southing component of a line.
17. For a line with length ‘L’ and Whole Circle Bearing ‘θ’, its Departure ‘D’ is given by:
Answer: D = L * sin(θ)
This is the standard trigonometric formula for calculating departure from length and WCB.
18. If a closed traverse has significant angular errors, which rule would generally be less suitable without prior angular adjustment?
Answer: Transit Rule
The Transit Rule assumes precise angular measurements. If angular errors are significant, they should be adjusted first before applying the Transit Rule for linear adjustments.
19. The linear error of closure (E) for a closed traverse represents:
Answer: The straight-line distance between the actual closing point and the starting point.
It is the vector sum of the errors in latitude and departure, indicating how much the traverse fails to close.
20. What is the fieldwork step in a theodolite traverse that involves taking lateral measurements to locate ground features?
Answer: Marking Offsets
Offsets are taken from the main traverse lines to detail surrounding features, creating a comprehensive map.