In civil engineering, curves are essential transitional elements connecting straight sections of roads, railways, and canals. They ensure smooth and safe changes in alignment or gradient, crucial for user comfort and structural integrity. This infographic provides a comprehensive overview of curve types, defines their fundamental elements, and explores the basic principles behind their design, offering key insights vital for any civil engineer involved in infrastructure development.
What are Curves in Surveying?
Curves are designed transitions provided at the intersection of two straight lines (tangents) to avoid abrupt changes in direction or gradient. They are fundamental in transportation design to ensure safety, comfort, and smooth flow.
Primary Classifications:
- Horizontal Curves: Provided in a horizontal plane to connect two tangents changing direction. (Generally circular)
- Vertical Curves: Provided in a vertical plane to connect two grades (slopes). (Generally parabolic)
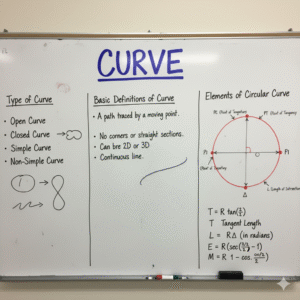
Types of Horizontal Curves
Horizontal curves are categorized based on their geometric characteristics and complexity, each suited for specific design situations.
| Curve Type | Description | Conceptual Diagram |
|---|---|---|
| Simple Circular Curve | An arc of a single circle, tangential to two straight lines (tangents). It has a constant radius throughout. | ⌒ |
| Compound Curve | Consists of two or more simple circular arcs of different radii, turning in the same direction, with their centers on the same side of the common tangent. | ∽ |
| Reverse Curve | Composed of two simple circular arcs of equal or different radii, turning in opposite directions, with their centers on opposite sides of the common tangent. Forms an ‘S’ shape. | S |
| Transition Curve (Spiral Curve) | A curve of varying radius, introduced between a tangent and a circular curve, or between two circular curves of different radii. Its radius varies from infinity to the radius of the circular curve. | 🌀 |
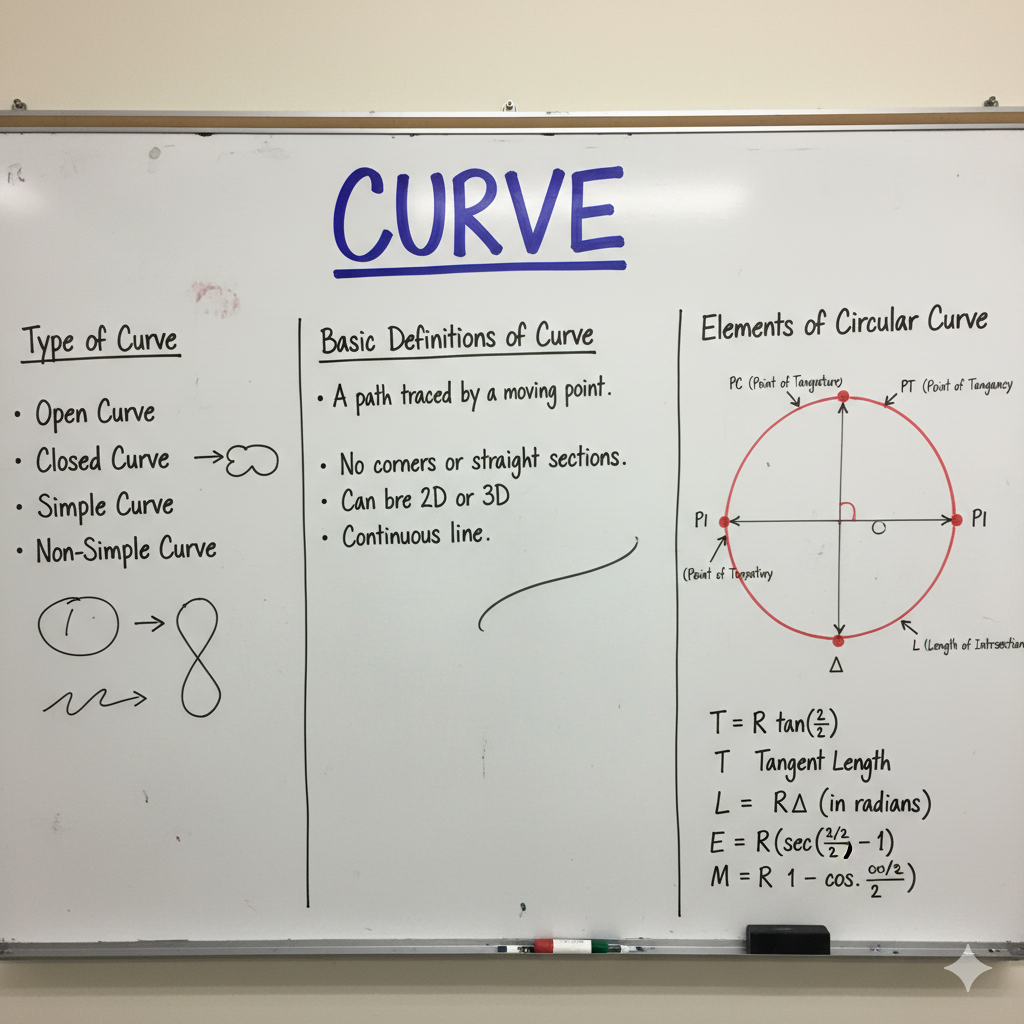
Basic Definitions of Curve Elements
Understanding the terminology associated with curves is fundamental to their design and layout.
| Term | Definition |
|---|---|
| Back Tangent (Rear Tangent) | The straight line (tangent) preceding the curve. |
| Forward Tangent (Front Tangent) | The straight line (tangent) following the curve. |
| Vertex (V) / Point of Intersection (PI) | The point where the back tangent and forward tangent intersect. |
| Deflection Angle (Δ) | The angle by which the forward tangent deflects from the back tangent. It is the angle between the two tangents. Also called the Angle of Intersection. |
| Point of Curvature (PC) / Tangent Point 1 (T1) | The point where the curve begins and the back tangent ends. |
| Point of Tangency (PT) / Tangent Point 2 (T2) | The point where the curve ends and the forward tangent begins. |
| Tangent Length (T) | The distance from the Vertex (PI) to either the PC (T1) or PT (T2). These lengths are equal for a simple circular curve. |
| Radius of Curve (R) | The radius of the circular arc forming the curve. (Constant for simple circular curve). |
Elements of a Simple Circular Curve & Their Formulas
The geometric elements of a simple circular curve are essential for its accurate setting out in the field. All calculations are based on the radius (R) and deflection angle (Δ).
| Element | Description | Formula |
|---|---|---|
| Tangent Length (T) | Distance from PI to PC or PT. | T = R tan(Δ/2) |
| Length of Curve (Lc) | The actual length of the circular arc from PC to PT. | Lc = (πRΔ) / 180° (if Δ in degrees) Lc = RΔ (if Δ in radians) |
| Long Chord (L) | The straight line distance connecting the Point of Curvature (PC) to the Point of Tangency (PT). | L = 2R sin(Δ/2) |
| External Distance (E) / Apex Distance | The distance from the Vertex (PI) to the midpoint of the curve along the bisector of the deflection angle. | E = R [sec(Δ/2) – 1] OR E = T tan(Δ/4) (approx) |
| Mid-Ordinate (M) / Versed Sine | The distance from the midpoint of the long chord to the midpoint of the curve, measured radially. | M = R [1 – cos(Δ/2)] |
Advantages & Disadvantages of Horizontal Curve Types
The choice of curve type significantly impacts design complexity, cost, and safety.
| Curve Type | Advantages | Disadvantages |
|---|---|---|
| Simple Circular Curve | Simple to design and set out. Constant radius provides consistent centrifugal force. | Abrupt change from straight to curve can cause discomfort, especially at high speeds, if no transition is provided. |
| Compound Curve | Can fit complex terrains where a simple curve is not feasible. Flexible in design. | More complex to design and set out. Abrupt change in curvature can cause discomfort if radii are significantly different. |
| Reverse Curve | Useful in restricted areas (e.g., railway sidings, congested urban roads) where space is limited for large single curves. | Extremely dangerous for high speeds as superelevation cannot be effectively provided throughout. Centrifugal force changes direction abruptly. |
| Transition Curve | Provides a gradual change in curvature and superelevation, enhancing comfort and safety at high speeds. Minimizes sudden jerks. | More complex to design and set out compared to simple circular curves. Requires more space. |
GATE Exam Practice Questions & Explanations
Test your understanding of Curves, their types, and elements with these GATE-style questions.
1. A curve connecting two straight lines (tangents) that is an arc of a single circle with a constant radius is known as a:
Answer: Simple Circular Curve
This is the basic definition of a simple circular curve, fundamental in horizontal alignment design.
2. The point where the back tangent and forward tangent intersect is called the:
Answer: Vertex (V) or Point of Intersection (PI)
This is a key geometric point in curve design, defining the intersection of the two straight segments.
3. For a simple circular curve with radius ‘R’ and deflection angle ‘Δ’, the tangent length (T) is given by:
Answer: T = R tan(Δ/2)
This formula is derived from the geometry of the circular curve, relating the radius and half the deflection angle to the tangent length.
4. A curve composed of two circular arcs of different radii, turning in the same direction, with their centers on the same side of the common tangent, is a:
Answer: Compound Curve
Compound curves are used when space constraints or terrain require a varying radius while maintaining the same direction of turn.
5. The distance from the midpoint of the long chord to the midpoint of the curve, measured radially, is known as the:
Answer: Mid-Ordinate (M) or Versed Sine
The mid-ordinate provides a measure of the curve’s “bulge” or deviation from the long chord.
6. Which type of curve forms an ‘S’ shape and consists of two circular arcs with their centers on opposite sides of the common tangent?
Answer: Reverse Curve
Reverse curves are characterized by their S-shape and are generally avoided at high speeds due to safety concerns related to superelevation.
7. The angle by which the forward tangent deflects from the back tangent is called the:
Answer: Deflection Angle (Δ) or Angle of Intersection
This angle defines the total change in direction that the curve provides.
8. What is the formula for the length of a circular curve (Lc) if the deflection angle ‘Δ’ is in degrees?
Answer: Lc = (πRΔ) / 180°
This formula calculates the arc length of the curve based on its radius and the central angle (which equals the deflection angle).
9. A curve of varying radius, introduced between a tangent and a circular curve, or between two circular curves of different radii, is a:
Answer: Transition Curve (Spiral Curve)
Transition curves provide a gradual change in curvature and superelevation, improving driver comfort and safety, especially at higher speeds.
10. The straight line distance connecting the Point of Curvature (PC) to the Point of Tangency (PT) is known as the:
Answer: Long Chord (L)
The long chord is a direct line segment across the curve, distinguishing it from the arc length.
11. Vertical curves are generally of what shape?
Answer: Parabolic
Parabolic curves are preferred for vertical alignment due to their ease of computation and consistent rate of change of grade.
12. The distance from the Vertex (PI) to the midpoint of the curve along the bisector of the deflection angle is the:
Answer: External Distance (E) or Apex Distance
This element represents the maximum offset of the curve from the point of intersection of the tangents.
13. Which type of horizontal curve is generally considered dangerous for high-speed traffic due to sudden changes in curvature and superelevation challenges?
Answer: Reverse Curve
The rapid reversal of curvature makes it difficult to provide continuous superelevation, posing a safety risk.
14. What is the primary purpose of providing a transition curve?
Answer: To provide a gradual change in curvature and superelevation.
This enhances comfort and safety by preventing abrupt jerks and allowing vehicles to smoothly adjust to the curve.
15. The point where a circular curve begins and the back tangent ends is called the:
Answer: Point of Curvature (PC) or Tangent Point 1 (T1)
This is the starting point of the circular arc on the plan.
16. For a simple circular curve, if the radius ‘R’ is 200m and the deflection angle ‘Δ’ is 60°, the tangent length (T) is approximately:
Answer: 115.47 m
T = R tan(Δ/2) = 200 * tan(60°/2) = 200 * tan(30°) = 200 * 0.57735 = 115.47 m.
17. The Point of Tangency (PT) is where:
Answer: The curve ends and the forward tangent begins.
This marks the end of the circular arc and the transition back to the straight alignment.
18. If the deflection angle ‘Δ’ of a simple circular curve is 90° and the radius ‘R’ is 100m, the long chord (L) is approximately:
Answer: 141.42 m
L = 2R sin(Δ/2) = 2 * 100 * sin(90°/2) = 200 * sin(45°) = 200 * 0.7071 = 141.42 m.
19. Which curve type consists of two or more circular arcs of different radii, turning in the same direction?
Answer: Compound Curve
The defining characteristic is multiple radii for curves turning in the same general direction.
20. The radius of a transition curve varies from:
Answer: Infinity to the radius of the circular curve.
At the tangent end, the curvature is zero (infinite radius), and it gradually decreases to match the radius of the main circular curve.