Tacheometry is a branch of surveying focused on rapid optical distance and elevation measurements. It eliminates the need for chaining or taping, making it invaluable for challenging terrains like hilly or rough ground where direct measurement is impractical. Utilizing a specialized theodolite (tacheometer) and a stadia rod, this method employs optical principles to derive distances and elevations quickly and efficiently. This infographic explores its theory, instrumentation, various measurement systems, and practical applications.
What is Tacheometry?
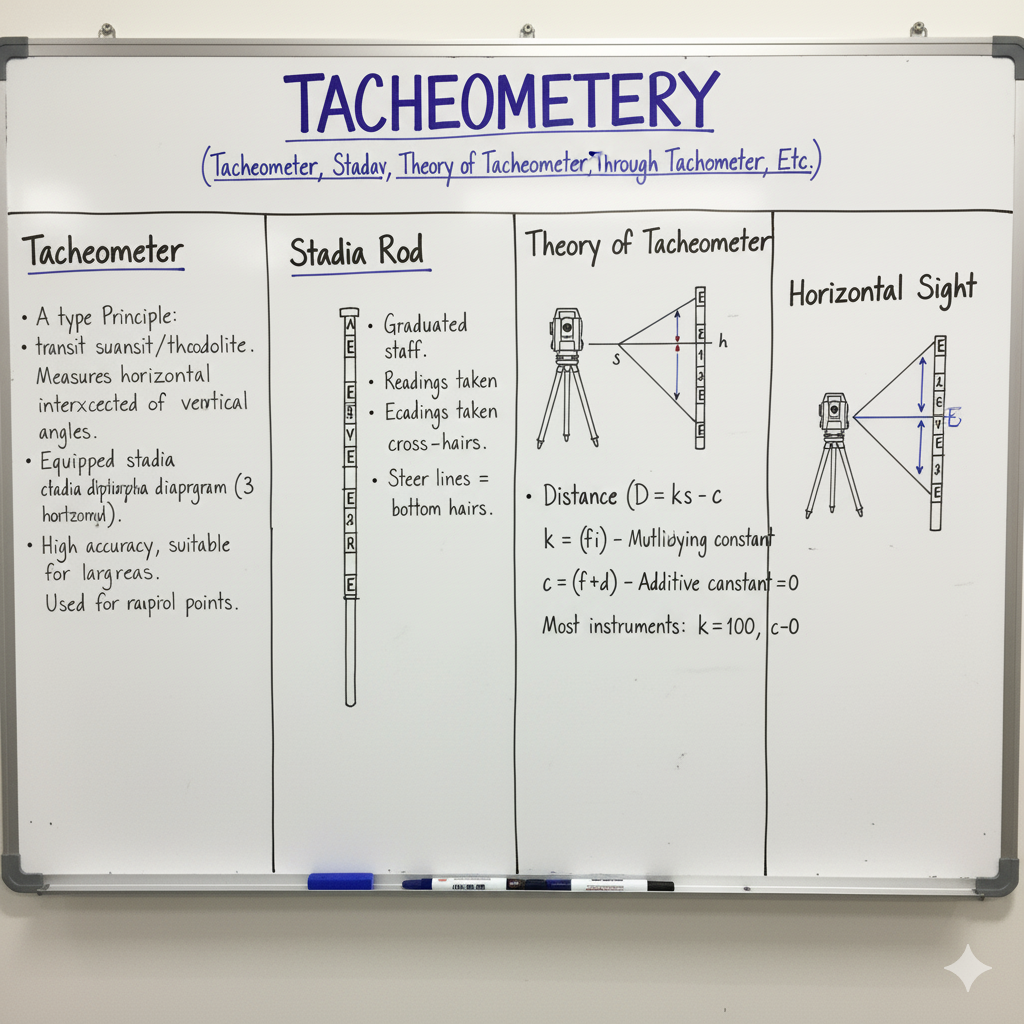
Tacheometry (or Stadia Surveying) is a method of surveying where horizontal distances and vertical elevations are determined indirectly by optical means, using an instrument called a tacheometer. It’s a rapid and convenient method, especially suited for rough terrain or areas where direct measurement is difficult or impossible.
The fundamental principle relies on the property that the ratio of the distance of the base from the focus to the length of the base is constant. In practice, this means the staff intercept observed through the tacheometer is proportional to the distance of the staff from the instrument.
Key Instruments in Tacheometry
Two primary instruments are essential for tacheometric surveying: a specialized theodolite and a uniquely graduated staff.
| Instrument | Description | Purpose in Tacheometry |
|---|---|---|
| Tacheometer | A special type of theodolite fitted with an anallactic lens and three horizontal stadia hairs (one central, two outer/stadia hairs) in its diaphragm. | Used for precise measurement of vertical and horizontal angles, and for observing staff intercepts for distance calculation. |
| Stadia Rod / Levelling Staff | A levelling staff (typically 3-5m long) used with a tacheometer. It must be very clearly and distinctly graduated, often with bold patterns, to facilitate accurate reading of stadia intercepts over long distances. | Provides a scale for reading the stadia interval (difference between upper and lower stadia hair readings) which is directly proportional to the distance. |
Systems of Tacheometric Measurement
Tacheometry employs different systems to determine distances and elevations, with the stadia system being the most common.
| System | Description | Sub-types/Principle |
|---|---|---|
| Stadia System | The most widely used system. It involves observing the intercept made by the stadia hairs on a stadia rod or staff. |
|
| Tangential System | Involves measuring two vertical angles to the top and bottom (or other specific points) of a staff of known length. | Distances and elevations are computed using trigonometric tangent functions. |
| Subtense Bar System | Uses a horizontal bar of fixed known length (subtense bar) set at the target station. The angle subtended by the bar at the instrument station is measured. | Primarily used for very accurate short-distance measurements. |
Theory of Tacheometer & Instrument Constants
The optical principle behind the tacheometer allows for the determination of horizontal distances and vertical intervals using two key constants.
Lens Formula & Derivation
The basic formula for a simple lens is 1/f = 1/v – 1/u, where ‘f’ is focal length, ‘v’ is image distance, and ‘u’ is object distance. Applying principles of similar triangles in the tacheometer’s optics, the relationship between horizontal distance (D), stadia interval (s), focal length (f), and distance from the optical center to the vertical axis of the instrument (c) is derived.
D = (f/i) × s + (f + c)
Tacheometric Constants:
- Multiplying Constant (K): K = f/i. For most tacheometers with anallactic lens, K = 100.
- Additive Constant (C): C = f + c. For most tacheometers with anallactic lens, C = 0.
Therefore, the fundamental tacheometric equation for horizontal distance becomes:
D = Ks + C
For anallactic lens, D = 100s (since C=0)
Distance & Elevation: Staff Vertical
This is the most common field procedure, where the stadia rod is held vertically at the target point.
Case 1: Line of Sight Horizontal
When the line of sight is perfectly horizontal, the horizontal distance and vertical height are straightforward.
Horizontal Distance (D) = Ks + C
RL of Staff Station = RL of Instrument Station + hi – Central Hair Reading
Case 2: Line of Sight Inclined
When sighting uphill or downhill, the measured stadia intercept is along the inclined line of sight. This requires correction to get the true horizontal distance and vertical height.
Horizontal Distance (D) = (Ks + C) cos2θ
Vertical Height (V) = (Ks + C) sinθ cosθ
Where θ = Vertical angle (elevation or depression)
RL of Staff Station = RL of Instrument Station + hi + V – Central Hair Reading (if sighted on staff)
Distance & Elevation: Staff Normal to Line of Sight
In some cases, especially on very steep slopes, the staff is held perpendicular to the line of sight to simplify calculations.
Procedure & Formula
When the staff is held normal (perpendicular) to the line of sight, the stadia intercept directly gives the length ‘s’ in the direction perpendicular to the line of sight.
Inclined Distance (L) = Ks + C
Horizontal Distance (D) = L cosθ
Vertical Height (V) = L sinθ
Where θ = Vertical angle
RL of Staff Station = RL of Instrument Station + hi ± V – [Central Hair Reading × cosθ]
(Adjust sign for V based on angle of elevation or depression)
Advantages & Disadvantages of Tacheometry
Tacheometry offers unique benefits but also has limitations compared to other surveying methods.
| Aspect | Advantages | Disadvantages |
|---|---|---|
| Speed | Very rapid method for obtaining both distances and elevations. Eliminates chaining/taping. | Less accurate than precise direct levelling or EDM for short, flat distances. |
| Terrain Suitability | Ideal for rough, hilly, or inaccessible terrain where chaining is difficult or impossible. | Accuracy can be affected by atmospheric conditions (refraction) over long sights. |
| Obstacles | Can easily measure across obstacles like rivers, valleys, or thick vegetation. | Requires clear line of sight to read staff, which can be obstructed by vegetation. |
| Cost | Can be more economical for certain types of surveys (e.g., topographic) over large areas. | Requires skilled operators and precise reading of stadia hairs. |
| Data Collection | Collects both horizontal and vertical data simultaneously. | Precision decreases significantly with increasing distance. |
GATE Exam Practice Questions & Explanations
Test your understanding of Tacheometry concepts and calculations with these GATE-style questions.
1. Tacheometry is a method of surveying in which:
Answer: Horizontal distances and vertical elevations are determined indirectly by optical means.
This is the defining characteristic of tacheometry, relying on optical principles rather than direct chaining or levelling.
2. The instrument used for tacheometry is a special theodolite fitted with:
Answer: Three horizontal stadia hairs in its diaphragm.
These stadia hairs (upper, middle, lower) are crucial for observing the staff intercept, which is then used to calculate distance.
3. For a tacheometer with an anallactic lens, the additive constant (C) is typically:
Answer: Zero
An anallactic lens is specifically designed to make the additive constant zero, simplifying the distance formula to D = Ks.
4. In the fixed hair method of tacheometry, the stadia interval (s) is:
Answer: Variable, depending on the distance to the staff.
With fixed stadia hairs, the difference in reading between the upper and lower hairs (stadia intercept) changes proportionally with the distance to the staff.
5. If the multiplying constant (K) of a tacheometer is 100, and the stadia intercept (s) is 1.5m for a horizontal line of sight, the horizontal distance (ignoring additive constant) is:
Answer: 150m
D = Ks = 100 * 1.5 = 150m.
6. Tacheometry is most advantageous for surveys on:
Answer: Hilly and rough ground
It avoids the difficulties of direct chaining or taping over uneven or steep terrain.
7. The system of tacheometric measurement that involves measuring two vertical angles to the top and bottom of a staff of known length is:
Answer: Tangential System
This system uses trigonometric tangent relationships based on the measured angles and known staff height.
8. If the line of sight is inclined by a vertical angle ‘θ’, and the staff is held vertical, the horizontal distance (D) is given by:
Answer: (Ks + C) cos2θ
This formula corrects the inclined stadia distance to its true horizontal component when the staff is vertical.
9. Which instrument constant in tacheometry is the ratio of the focal length of the objective lens to the stadia interval?
Answer: Multiplying Constant (K = f/i)
This constant, typically 100, relates the observed staff intercept to the inclined distance.
10. A stadia rod used in tacheometry must be:
Answer: Clearly and distinctly graduated to facilitate accurate readings.
The precision of stadia readings depends on the clarity of the staff graduations, especially at long distances.
11. What is the main advantage of the stadia system (fixed hair method) over other tacheometric systems?
Answer: Simplicity and speed in fieldwork.
It allows for rapid distance determination by simply reading the staff intercept, without complex angular measurements or specialized targets.
12. If the staff is held normal (perpendicular) to the line of sight, and the inclined distance calculated is ‘L’, then the horizontal distance (D) is:
Answer: L cosθ
When the staff is normal, the calculated distance ‘L’ is the inclined distance, which then needs to be converted to horizontal distance using the vertical angle.
13. The stadia system is broadly classified into Fixed hair method and:
Answer: Movable hair method
In the movable hair method, the stadia hairs are adjusted to subtend a constant intercept on the staff, and the distance is a function of the angle subtended by the hairs.
14. When determining elevation with an inclined line of sight and staff vertical, the vertical height (V) from the instrument axis to the central hair reading is:
Answer: (Ks + C) sinθ cosθ
This formula accounts for both the inclined distance and the angle of inclination to get the vertical component of the line of sight to the staff.
15. The distance from the optical center of the objective lens to the vertical axis of the instrument is represented by which constant in the tacheometric theory?
Answer: ‘c’ (part of the additive constant C = f + c)
The distance ‘c’ is the offset from the objective lens to the trunnion axis, forming part of the additive constant.
16. Tacheometry is generally NOT as accurate as:
Answer: Direct levelling or EDM measurements for short distances.
For very high precision over short to medium distances, direct methods or Electronic Distance Measurement (EDM) often provide superior accuracy compared to tacheometry.
17. What type of lens is commonly used in tacheometers to simplify the distance formula?
Answer: Anallactic lens
The anallactic lens makes the additive constant ‘C’ equal to zero, simplifying the distance formula to D = Ks.
18. The subtended angle in the Subtense Bar System is measured at the:
Answer: Instrument station
The instrument measures the angle formed by sighting the two ends of the subtense bar placed at the target station.
19. If RL of instrument station is 100m, hi is 1.5m, central hair reading is 2.0m, and calculated vertical height (V) is +5.0m, what is the RL of the staff station?
Answer: 104.5m
RLstaff = RLinstrument + hi + V – Central Hair Reading = 100 + 1.5 + 5.0 – 2.0 = 104.5m.
20. The principal advantage of tacheometry over chain or tape surveying is:
Answer: Its speed and applicability in difficult terrains.
Tacheometry significantly reduces fieldwork time and effort, especially when direct measurement with chain or tape is impractical due to obstacles or steep slopes.