After the design of a circular curve is complete, the next critical step in civil engineering projects is its accurate physical realization on the ground. This process, known as “setting out,” involves transferring the designed curve from paper plans to the actual terrain. Precision in setting out curves is paramount for ensuring smooth transitions, safe vehicle movement, and the structural integrity of roads, railways, and canals. This infographic details the primary linear and angular methods employed for this crucial task.
What is Setting Out a Curve?
Setting out a curve involves accurately locating and marking specific points of the designed circular arc on the ground. This process translates the calculated geometric elements of the curve into physical points that guide construction.
The choice of method depends on factors such as the required accuracy, the length of the curve, available equipment, and ground conditions. Proper setting out ensures that the constructed curve matches the design specifications precisely.
Broad Classification of Setting Out Methods
Methods for setting out circular curves are broadly categorized based on the primary type of measurement used in the field.
| Category | Description | Primary Measurement |
|---|---|---|
| Linear Methods | Involve setting out points on the curve by measuring distances (offsets) from a reference line, using only tapes or chains. | Distances |
| Angular Methods | Involve setting out points on the curve by measuring angles (deflection angles or tangential angles) from a tangent, often in conjunction with distances, using instruments like a theodolite. | Angles (and Distances) |
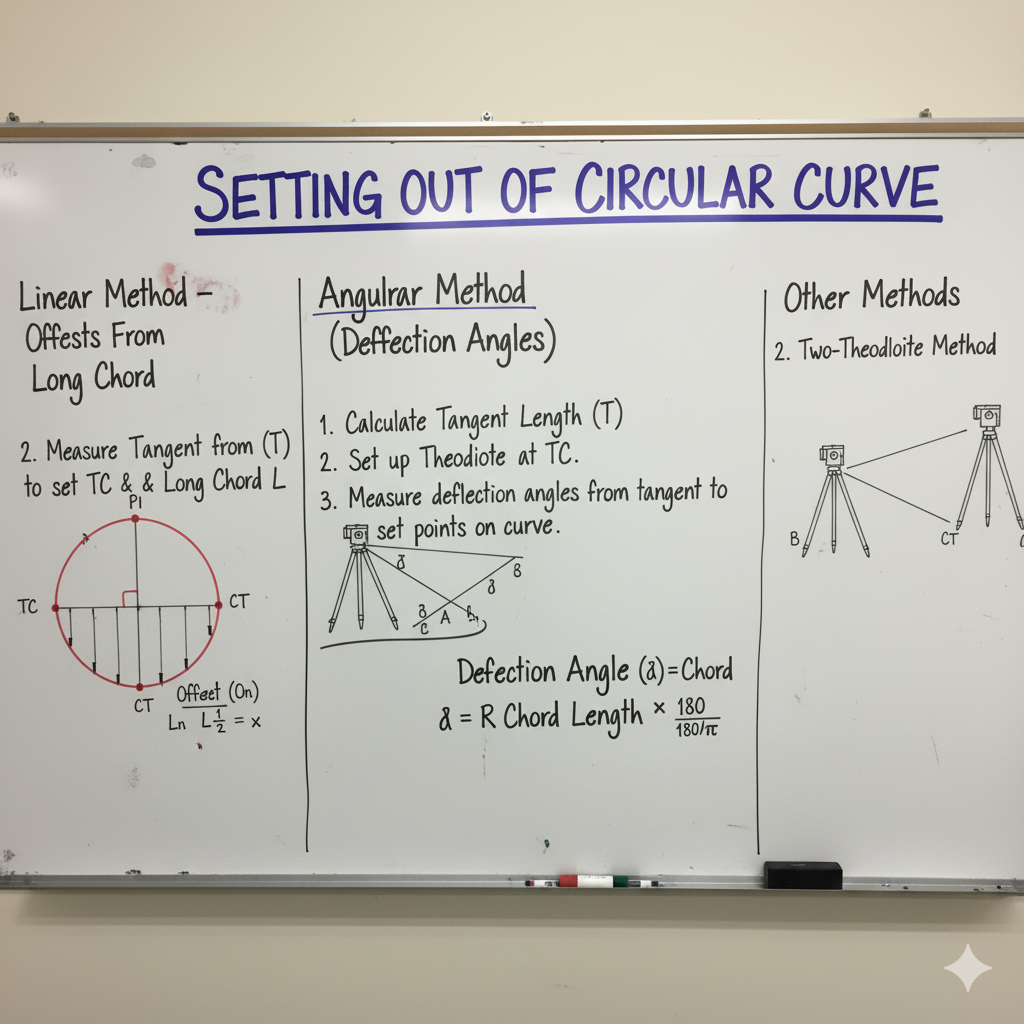
Linear Methods for Setting Out Curves
These methods rely primarily on direct linear measurements (offsets) from tangents or chords to locate points on the curve. They are generally simpler but may be less accurate for long curves.
1. Offsets from Tangent (Perpendicular & Radial)
| Method | Principle | Formula |
|---|---|---|
| Perpendicular Offset from Tangent (Ox) | Offsets are measured perpendicular to the tangent line at various points along the tangent. | Ox = x2 / (2R) (for small ‘x’, where x is distance along tangent) |
| Radial Offset from Tangent (Or) | Offsets are measured radially (towards the center of the curve) from the tangent. | Or = R – sqrt(R2 – x2) |
2. Offsets from Long Chord
| Method | Principle | Formula |
|---|---|---|
| Offsets from Long Chord (Ox) | Points on the curve are located by measuring offsets perpendicular from the long chord. The mid-ordinate is a key reference. | Ox = sqrt(R2 – x2) – (R – M) (where x is distance from midpoint of long chord) |
| Mid-Ordinate (M) of Long Chord | The offset at the center of the long chord. | M = R(1 – cos(Δ/2)) |
3. Offsets from Chord Produced
| Method | Principle | Formula |
|---|---|---|
| Offsets from Chord Produced (On) | Points on the curve are set out by extending the previously set chord and measuring an offset from this extension. | On = (Cn-1 * Cn) / (2R) (approx, for next chord, C is chord length) |
Angular Methods for Setting Out Curves
These methods utilize a theodolite to measure angles, offering higher precision and suitability for longer curves or difficult terrain.
1. Rankine’s Method of Tangential Angles (Deflection Angles)
| Principle | Key Formula | Procedure |
|---|---|---|
| Points on the curve are located by measuring angles from the tangent at PC (or PT) and distances along a chord. | δn = (1718.9 * c) / R minutes OR δn = (c / (2R)) radians (δn is tangential angle for chord ‘c’) |
Set up theodolite at PC, sight along tangent. Deflect angle δ1 to locate 1st point (P1) by measuring chord C1. Then deflect δ2 from P1 to P2, etc. |
2. Two-Theodolite Method
| Principle | Procedure | Advantages |
|---|---|---|
| Two theodolites are simultaneously set up at PC and PT. Angles are turned from both ends to fix points by intersection. | Set up 1st theodolite at PC, 2nd at PT. Turn angles from tangent at PC and from long chord at PT. Intersect lines of sight to locate points. | Highly accurate. Suitable for rough ground and long curves where chaining is difficult. |
3. Tacheometric Method
| Principle | Application |
|---|---|
| Uses a tacheometer to measure both angles and distances (via stadia readings) to locate points on the curve. | Efficient for setting out curves in broken or hilly terrain where direct chaining is impractical, often used for preliminary surveys. |
Comparison of Linear vs. Angular Methods
The choice between linear and angular methods depends on desired accuracy, site conditions, and available resources.
| Feature | Linear Methods | Angular Methods |
|---|---|---|
| Accuracy | Generally less accurate for long curves; accuracy decreases with distance from tangent/chord. | More accurate, especially for long curves; errors in angle measurement are less cumulative. |
| Speed | Can be slow for very long curves due to many offset measurements. | Generally faster for long curves, especially Two-Theodolite method. |
| Equipment | Only tape/chain and pegs. Simple instruments. | Theodolite(s), tape/chain (for chords), ranging rods. More complex instruments. |
| Terrain Suitability | Best for flat, open ground. Difficult on rough/hilly terrain. | Highly suitable for rough, hilly, or obstructed terrain. |
| Visibility | Requires clear visibility for measuring offsets. | Requires clear line of sight for angular measurements between stations. |
Key Instruments Used for Setting Out Curves
Modern surveying utilizes various instruments to achieve precision in setting out curves.
| Instrument/Method | Primary Role | Typical Use Case |
|---|---|---|
| Tape Method | Direct linear measurement of offsets and chord lengths. | Simple curves, short lengths, when high precision is not paramount. |
| Tape & Theodolite Method | Theodolite for angular setup, tape for chord lengths. | Common method (e.g., Rankine’s), good balance of accuracy and efficiency. |
| Two-Theodolite Method | Two theodolites used simultaneously for precise angular intersection. | Long curves, high accuracy required, difficult terrain. |
| Tacheometric Method | Tacheometer for simultaneous distance and angle measurement. | Rough/hilly terrain, reconnaissance, where rapid work is needed. |
| Total Station Method | Integrated EDM, theodolite, and onboard computer for coordinates and setting out. | Highly precise, modern method for all types of curves, very efficient. |
GATE Exam Practice Questions & Explanations
Test your understanding of curve setting out methods with these GATE-style questions.
1. Which of the following is a linear method for setting out a circular curve?
Answer: Offsets from Long Chord
Linear methods rely solely on distance measurements, like offsets from a long chord, tangent, or produced chord.
2. Rankine’s Method for setting out a circular curve is classified as a(n):
Answer: Angular Method
Rankine’s method involves calculating and setting out tangential angles using a theodolite, making it an angular method.
3. For setting out curves by the method of perpendicular offsets from the tangent, the offset Ox at a distance ‘x’ from PC along the tangent, for a curve of radius ‘R’, is approximately given by:
Answer: Ox = x2 / (2R)
This is the standard approximate formula for perpendicular offsets from the tangent, valid for small values of x.
4. Which method of setting out a circular curve involves the simultaneous use of two theodolites?
Answer: Two-Theodolite Method
In this highly accurate angular method, one theodolite is at PC and the other at PT, and points are fixed by intersecting lines of sight.
5. The primary advantage of angular methods over linear methods for setting out curves is:
Answer: Higher accuracy, especially for long curves.
Angular methods are less susceptible to cumulative errors over long distances and rough terrain compared to relying solely on linear measurements.
6. When setting out a curve by offsets from the long chord, the maximum offset occurs at the:
Answer: Midpoint of the long chord
This maximum offset is also known as the mid-ordinate or versed sine of the curve.
7. The formula for tangential angle δn for a chord ‘c’ and radius ‘R’ (in radians) in Rankine’s Method is:
Answer: δn = c / (2R)
This formula is derived from the geometric relationship between the tangential angle, chord length, and radius.
8. Which linear method is generally considered suitable for rough ground and long curves where chaining is difficult?
Answer: None of the standard linear methods are ideal for rough ground and long curves. Angular methods are preferred.
Linear methods become impractical and less accurate on rough or undulating terrain, making angular methods more suitable.
9. In the Two-Theodolite Method, where are the two theodolites typically set up?
Answer: At the Point of Curvature (PC) and the Point of Tangency (PT)
This strategic placement allows for simultaneous angular measurements from both ends of the curve.
10. The process of marking specific points of the designed circular arc on the ground is known as:
Answer: Setting Out (or Laying Out)
Setting out is the field process of translating design plans into physical ground markers for construction.
11. For a curve of radius R, the radial offset Or at a distance ‘x’ along the tangent is given by:
Answer: Or = R – sqrt(R2 – x2)
This formula calculates the offset along a radial line from the tangent to the curve.
12. Which angular method is particularly efficient for setting out curves in broken or hilly terrain where direct chaining is impractical?
Answer: Tacheometric Method
Tacheometry allows for simultaneous measurement of distances and angles optically, making it ideal for difficult terrains without direct chaining.
13. In Rankine’s method, the deflection angle for any point on the curve from the PC is equal to:
Answer: The tangential angle from the PC to that point.
The method directly uses the tangential angles, which are essentially deflection angles turned from the tangent at the PC.
14. What instrument is commonly used in Tape & Theodolite Method for setting out curves?
Answer: Theodolite and Tape
The theodolite is used for angular measurements, and the tape for linear chord measurements.
15. The method of offsets from chord produced is generally considered:
Answer: Less accurate than offsets from tangent for longer chords.
Errors tend to accumulate more rapidly when extending chords, leading to lower accuracy over longer segments.
16. The modern, highly precise method for setting out all types of curves, integrating EDM, a theodolite, and onboard computing, is the:
Answer: Total Station Method
Total stations provide unparalleled accuracy and efficiency for complex curve setting out.
17. What is the main disadvantage of linear methods for setting out long curves?
Answer: Accuracy decreases with distance from the tangent or chord.
Errors in measuring offsets accumulate, making it difficult to maintain high precision over extended curve lengths.
18. In the Two-Theodolite Method, how are the points on the curve located?
Answer: By intersection of lines of sight from two theodolites at PC and PT.
The simultaneous angular measurements define the unique position of each point on the curve.
19. Which method is simplest to apply when only a tape or chain is available?
Answer: Linear methods (e.g., offsets from tangent)
These methods do not require angular instruments, relying solely on basic linear measurements.
20. For which type of terrain are angular methods for setting out curves highly suitable?
Answer: Rough, hilly, or obstructed terrain
Angular methods minimize reliance on direct ground measurements, making them ideal for challenging topographical conditions.